1008. Construct Binary Search Tree from Preorder Traversal

Problem Statement

Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.

It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.

A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.

A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.

Example 1:

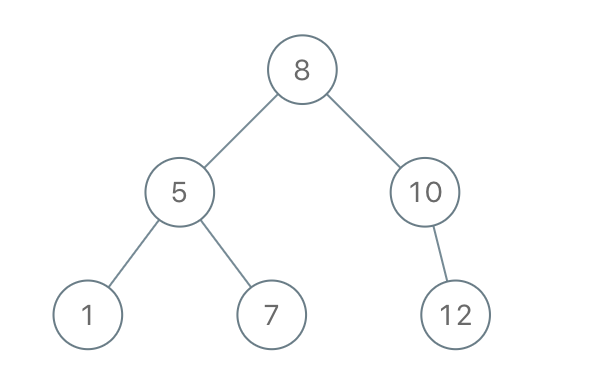
Input: preorder = [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

Example 2:

Input: preorder = [1,3]
Output: [1,null,3]

Constraints:

• 1 <= preorder.length <= 100

• 1 <= preorder[i] <= 1000

• All the values of preorder are unique.

Intuition

Make an inorder, as BST so sorted of preorder

And apply the same concept of construction. By recursively building the tree

Links

https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/

Video Links

Approach 1:

C++

class Solution {
public:
    unordered_map<int, int> mp;
    TreeNode* Tree(vector<int>& preorder, int p_start, int p_end, vector<int>& inorder, int in_start, int in_end){
        if(in_start > in_end)
            return nullptr;

        TreeNode* root = new TreeNode(preorder[p_start]);
        int index = mp[preorder[p_start]];
        int diff = index - in_start;

        root->left = Tree(preorder, p_start+1, p_start+diff, inorder, in_start, index-1);
        root->right = Tree(preorder, p_start+diff+1, p_end, inorder, index+1, in_end);

        return root;
    }

    TreeNode* bstFromPreorder(vector<int>& preorder) {
        vector<int> inorder(preorder);
        sort(inorder.begin(), inorder.end());

        for(int i=0;i<inorder.size(); i++)
            mp[inorder[i]] = i;
    
        return Tree(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1);
    }
};

Approach 2:

C++

Approach 3:

C++

Approach 4:

C++

Similar Problems