1424. Diagonal Traverse II

Problem Statement

Given a 2D integer array nums, return all elements of nums in diagonal order as shown in the below images.

Example 1:

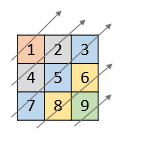
Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
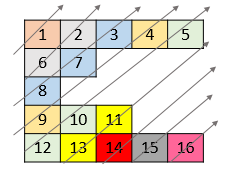
Output: [1,4,2,7,5,3,8,6,9]

Example 2:

Input: nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
Output: [1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

Constraints:

• 1 <= nums.length <= 105

• 1 <= nums[i].length <= 105

• 1 <= sum(nums[i].length) <= 105

• 1 <= nums[i][j] <= 105

Intuition

Approach:1

Note that in forward daigonal the sum of i+j at particular daigonal is same
We can use this, Maintain  a map for this
(If we want backward daigonal then difference of i+j)

Tc =O(N) SC = O(N)

Approach: 2
BFS kind

Push the element to the left and bottom at each place
TC - O(N) ; SC = O(root(N)) Daigonal in the queue in worst case

Links

https://leetcode.com/problems/diagonal-traverse-ii/description/?envType=daily-question&envId=2023-11-22

Video Links

https://www.youtube.com/watch?v=5hG2nDEiwlE&ab_channel=AryanMittal

Approach 1:

C++

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& nums) {
        int maxKey=0;
        vector<int> ans;
        unordered_map<int, vector<int>> mp;

        for(int i=nums.size()-1; i>=0; i--){
            for(int j=0; j<nums[i].size(); j++){
                mp[i+j].push_back(nums[i][j]);
                maxKey = max(maxKey, i+j);
            }
        }

        for(int i=0; i<=maxKey; i++){
            for(auto &it: mp[i]){
                ans.push_back(it);
            }
        }

        return ans;
    }
};

Approach 2:

C++

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& nums) {
        int n = nums.size();
        queue<pair<int,int>> q;
        vector<int> ans;
        q.push({0,0});

        while(!q.empty()){
            int size = q.size();

            for(int i=0; i<size; i++){
                int row = q.front().first;
                int col = q.front().second;
                ans.push_back(nums[row][col]);
                q.pop();

                if(col==0 and row+1<n){
                    q.push({row+1,col});
                }

                if(col+1 < nums[row].size()){
                    q.push({row,col+1});
                }
            }
        }

        return ans;
    }
};

Approach 3:

C++

Approach 4:

C++

Similar Problems