662. Maximum Width of Binary Tree

Problem Statement

Given the root of a binary tree, return the maximum width of the given tree.

The maximum width of a tree is the maximum width among all levels.

The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.

It is guaranteed that the answer will in the range of a 32-bit signed integer.

Example 1:

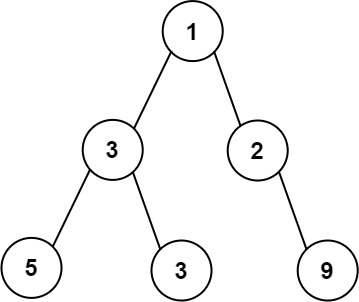
Input: root = [1,3,2,5,3,null,9]
Output: 4
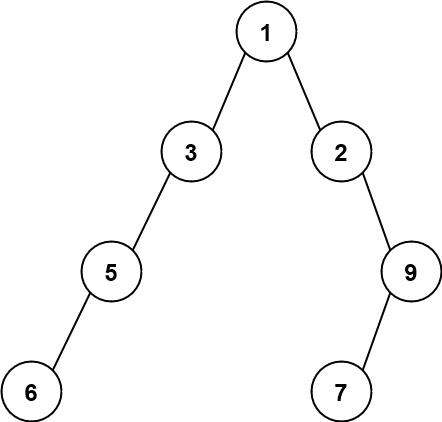
Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).

Example 2:

Input: root = [1,3,2,5,null,null,9,6,null,7]
Output: 7
Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).

Example 3:

Input: root = [1,3,2,5]
Output: 2
Explanation: The maximum width exists in the second level with length 2 (3,2).

Constraints:

• The number of nodes in the tree is in the range [1, 3000].

• -100 <= Node.val <= 100

Intuition

Approach:

1) Do a BFS traversal, as we want the width, builing the intuition
2) Now, we can index the tree nodes like

   0
  / \
  1 2
  .. son

if index = i
Left = 2*i+1
right = 2*i+2

in 0 based indexing

now we can maintain a queue to track the indices

Now to avoid overflow, We do a trick 
For skewed tree, i - 2i - 4i .. can cause overflow

So mmin trick

Links

https://leetcode.com/problems/maximum-width-of-binary-tree/description/

Video Links

https://www.youtube.com/watch?v=ZbybYvcVLks&ab_channel=takeUforward

Approach 1:

C++

class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) {
        queue<pair<TreeNode*, long long int>> q;
        q.push({root, 0});
        long long int len=0;

        while(!q.empty()){
            int size = q.size();
            int mmin = q.front().second;
            long long int left, right;
            
            for(int i=0; i<size; i++){
                TreeNode* temp = q.front().first;
                long long int index = q.front().second;

                if(i==0)
                    left = index;
                if(i==size-1)
                    right = index;

                if(temp->left){
                    long long int node_idx = (2*index+1) - mmin;
                    q.push({temp->left, node_idx}); 
                }
                if(temp->right){
                    long long int node_idx = (2*index+2) - mmin;
                    q.push({temp->right, node_idx}); 
                }
                q.pop();
            }
            len = max(len, right-left+1);
        }

        return len;
    }
};

Approach 2:

C++

Approach 3:

C++

Approach 4:

C++

Similar Problems