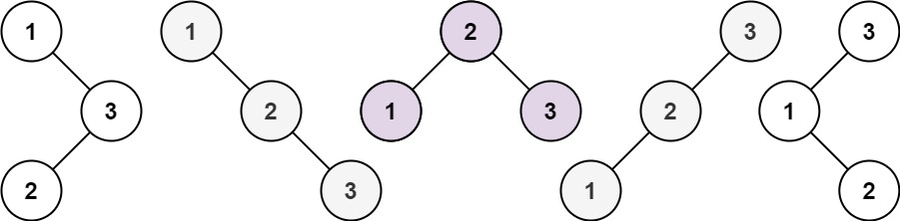
96. Unique Binary Search Trees

Problem Statement

Given an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from 1 to n.

Example 1:

Input: n = 3
Output: 5

Example 2:

Input: n = 1
Output: 1

Constraints:

• 1 <= n <= 19

Intuition

Approach 1: Formula

        /*
        2n
         C
          n
        ----
        (n+1)

        Catalan number

        Since Double loses precision 
        We use repetative approach to calculate

        nCk

        6C3 = 6*5*4/3*2*1
        Run for 1 to k  
        at each step multiply by n and divide by 1
        */

Approach 2 :

Using Dp

Lets take n = 2
  1 2 
Root as 1 ; Left = 0 right = 1 elements
Root as 2 ; Left = 1 right = 0 elements

n = 3
0 2
1 1
2 0
Add all 

So on

Total n elements -> i ) 1 ( n-i-1 

Links

https://leetcode.com/problems/unique-binary-search-trees/description/

Video Links

Approach 1:

Catalan Formula Approach

C++

class Solution {
public:
    int numTrees(int n) {
        long long ans = 1;
        int x = 2*n;

        for(int i=1; i<=n; i++){
            ans *= x;
            x--;
            ans /= i;
        }

        return ans / (n+1);

        /*
        2n
         C
          n
        ----
        (n+1)

        Catalan number

        Since Double loses precision 
        We use repetative approach to calculate

        nCk

        6C3 = 6*5*4/3*2*1
        Run for 1 to k  
        at each step multiply by n and divide by 1
        */
    }
};

Approach 2:

Memoization    

C++

class Solution {
public:
    unordered_map<int,int> mp;
    int numTrees(int n) {
        if(n == 1 or n == 0)
            return 1;

        if(mp.find(n) != mp.end())
            return mp[n];

        int ans = 0;

        for(int i=0; i<n; i++)
            ans += numTrees(i) * numTrees(n-i-1);

        return mp[n] = ans;
    }
};

Approach 3:

C++

Approach 4:

C++

Similar Problems